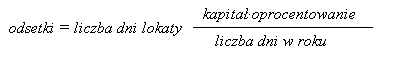| Arkusz 1 |
 |
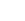| Zadanie 1 (3 pkt.) |
a) Rozwiaz nierównosc x2 < 4.
b) Ze zbioru rozwiazan tej nierównosci wybierz i wypisz wszystkie liczby naturalne
|
|
| Zadanie 2 (5 pkt.) |
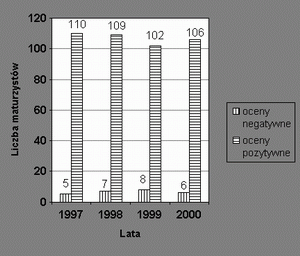Obok, na wykresie, pokazano wyniki egzaminu maturalnego z matematyki w pewnej szkole, w ciagu ostatnich 4 lat. Korzystajac z tych danych:
- odczytaj i zapisz, w którym roku mature z matematyki zdawalo najwiecej uczniów. Ilu ich bylo?
- oblicz, ile procent uczniów zdalo mature z matematyki w 2000 roku,
- oblicz, ile procent uczniów nie zdalo matury z matematyki w ciagu calego omawianego okresu 4 lat.
|
|
| Zadanie 3 (3 pkt.) |
Cena pewnego towaru wraz z 7% stawka podatku VAT byla równa 64,20 zlotych.
Oblicz cene tego towaru gdyby stawka podatku VAT byla równa 22% zamiast 7%
|
|
| Zadanie 4 (3 pkt.) |
Aby obliczyc odsetki od kapitalu bankowcy stosuja nastepujacy wzór:
UWAGA: W zaleznosci od banku przyjmuje sie, ze liczba dni w roku równa sie 360 albo 365. Notuje sie wówczas odsetki 360 albo odsetki 365. Dysponujesz kapitalem 10 000 zlotych, który chcialbys ulokowac na 60 dni. W dwóch bankach oprocentowanie jest takie samo i równa sie 15%, zas liczbe dni w roku jeden bank przyjmuje jako 360, drugi jako 365.
Stosujac powyzszy wzór oblicz odsetki od podanego kapitalu w kazdym z tych banków.
Która lokata jest korzystniejsza i o ile zlotych?
|
|
| Zadanie 5 (3 pkt.) |
W pewnym barze jeden paczek kosztuje p zlotych, zas jeden napój n zlotych. Za 4 paczki i 5 napojów zaplacimy w tym barze 11,55 zlotych.
a) Zapisz za pomoca równania koszt 4 paczków i 5 napojów w tym barze.
b) Oblicz, ile zaplacimy w tym barze za 1 napój, jesli jeden paczek kosztuje 1,20 zlotych.
|
|
| Zadanie 6 (3 pkt.) |
W ponizszej tabelce pokazano kurs sprzedazy marki niemieckiej w dniu 30.01.2001 r. w wybranych 50 kantorach w naszym kraju.
| Kurs sprzedazy (w zlotych) |
1,99 |
2,01 |
2,02 |
2,05 |
| Liczba kantorów |
30 |
15 |
3 |
2 |
- Uwzgledniajac podane liczby kantorów, oblicz sredni kurs sprzedazy marki niemieckiej w tym dniu.
- Podaj liczbe kantorów, w których tego dnia kurs sprzedazy marki niemieckiej byl nizszy od obliczonego
|
|
| Zadanie 7 (4 pkt.) |
|
Pewna firma, specjalizujaca sie w kopaniu studni, oferuje klientom nastepujacy sposób obliczania kosztu robót ziemnych: wykopanie pierwszego metra glebokosci studni kosztuje 300 zlotych, zas wykopanie kazdego nastepnego metra glebokosci kosztuje o 30 zlotych wiecej niz poprzedniego metra. Sprawdz, czy 7500 zlotych wystarczy, aby zaplacic tej firmie za wydrazenie studni o glebokosci 15 metrów.
|
|
| Zadanie 8 (4 pkt.) |
|
Ciag liczbowy (an) jest okreslony wzorem an = n + n2 Wykaz, ze jest to ciag rosnacy
|
|
| Zadanie 9 (3 pkt.) |
Wierzcholkami trójkata ABC sa punkty A (-3, -4), B (-2, 1), C (3, 0).
a) Sprawdz, ze |AB|=|BC|
b) Uzasadnij, ze kat ABC jest katem prostym
|
|
| Zadanie 10 (3 pkt.) |
|
Na okregu dany jest zbiór 5 róznych punktów. Ile jest róznych wielokatów, których wierzcholki naleza do danego zbioru? (Wielokaty sa rózne, jezeli róznia sie przynajmniej jednym wierzcholkiem. )
|
|
| Zadanie 11 (6 pkt.) |
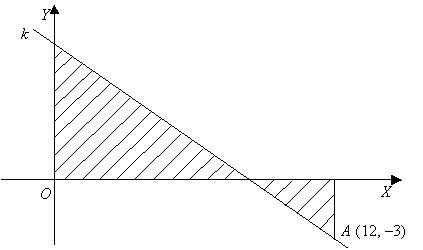
Na rysunku powyzej, prosta k przechodzi przez punkt A (12, -3). Wiedzac, ze stosunek pól obu zakreskowanych trójkatów prostokatnych jest równy 4:
a) oblicz sume pól tych trójkatów,
b) wyznacz równanie prostej k.
|
|
|
|
 |
|
Jakie wybrać studia?
